Trigonometry

Notation

When writing down an angle, the convention is to give degrees to 1 decimal place, and radians to 4 significant figures.

Convert polar to rectangular coordinates

Where 0\degree \leq \theta \leq 90\degree:

x = r \cos \theta \\ y = r \sin \theta

When 90\degree \le \theta \leq 180\degree, we use 180\degree - \theta as the angle and negate the result:

x = -r \cos (180\degree - \theta) \\ y = r \sin \theta

The angle used must always be the acute angle made with the x axis. The following diagram shows which ratio is positive in each quadrant:

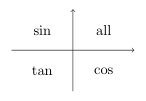
Finding angle of point to x-axis

Draw the point and angle on a pair of axis, label the opposite and adjacent with lengths (which are always positive), use \tan^{-1}(\frac{y}{x}) to find this angle, and then offset the angle to the correct quadrant as needed.

Definition of tan

\tan \theta = \frac{\sin \theta}{\cos \theta} = \frac{r \sin \theta}{r \cos \theta} = \frac{y}{x}
y = x \tan \theta

Convert between degrees and radians

To convert degrees to radians (equation looks like a d):

r = d \times \frac{\pi}{180}

To convert radians to degrees (equation looks like an r):

d = r \times \frac{180}{\pi}

We can also see this as converting the unit to turns and then converting from turns to the target unit. For radians to degrees, we divide by 2\pi (the number of radians in a turn), and then multiply by 360 (the number of degrees in a turn):

d = r \times \frac{360}{2\pi}

Calculate arc length

The arc length subtended by an angle of \theta radians in a circle of radius r is r \times \theta.

If the angle is given in degrees, first convert to radians.

Special triangles

The 1 : 1 : \sqrt{2} triangle has angles 45\degree and 45\degree (\frac{\pi}{4} and \frac{\pi}{4}).

The 1 : 2 : \sqrt{3} triangle has angles 30\degree and 60\degree (\frac{\pi}{6} and \frac{\pi}{3}).

Graphing the trigonometric functions

\sin has range [-1, 1], period 2\pi, and y-intercept 0.

\cos has range [-1, 1], period 2\pi, and y-intercept 1. It is the same as \sin shifted left by 90\degree.

\tan has period \pi, with y = 0 at each multiple of \pi and asymptotes midway between each multiple of \pi.

Inverse trigonometric functions

\theta = \sin^{-1} (\sin \theta) \\ \theta = \cos^{-1} (\cos \theta) \\ \theta = \tan^{-1} (\tan \theta)

Power notation

When the power is -1, the notation is overloaded to instead mean the corresponding inverse trigonometric function.

\sin^{n} \theta = (\sin \theta)^{n}

Solving trigonometric equations

Take the following equation:

\cos \theta = -0.4

We start by drawing the line x = -0.4 over the unit circle. If the function were \sin, we’d draw y = -0.4. If the function were \tan, we’d draw y = 0.4x (from \frac{y}{x} = 0.4). Mark the two intersection points, and draw radii to them. We’re looking for the angles to each of those radii from the positive x-axis.

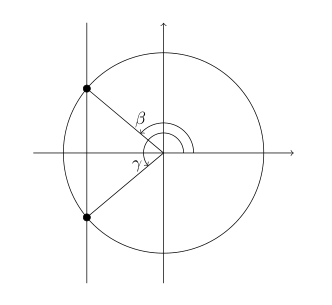
Next, calculate the closest angle to either radii from the x-axis with \arccos(0.4). We drop the sign here, because the inverse functions only act in the first quadrant. This yields 1.159 (to 4 significant figures). If the ratio can be found on one of the special triangles, it’s best to use it to find the angle in terms of \pi.

Finally, we offset the angle into the correct quadrants and find x to be \pi - 1.159, \pi + 1.159. The MATHS 102 coursebook rounds the angles immediately, not waiting until the end.

Addition identities

How to derive these identities

\sin(x+y) = \sin x \cos y + \cos x \sin y \\ \sin(x-y) = \sin x \cos y - \cos x \sin y
\cos(x+y) = \cos x \cos y - \sin x \sin y \\ \cos(x-y) = \cos x \cos y + \sin x \sin y
\tan(x+y) = \frac{\tan x + \tan y}{1 - \tan x \tan y}
\tan(x-y) = \frac{\tan x - \tan y}{1 + \tan x \tan y}

When solving a \tan equation, if either x or y is not defined, use the following instead:

\tan(x-y) = \frac{\sin(x-y)}{\cos(x-y)}

When deriving the \tan equation from \tan\theta = \frac{\sin\theta}{\cos\theta}, expand the \sin and \cos as above, and then split the terms and divide every term in the fraction by \cos\theta\cos\phi. Finally, cancel factors and simplify.

Double-angle identities

Derived from f(\theta + \theta):

\sin 2\theta = 2 \sin \theta \cos \theta \\ \cos 2\theta = \cos^2 \theta - \sin^2 \theta
\tan 2\theta = \frac{2\tan\theta}{1-\tan^2\theta}

Further, because 1 = \cos^2 \theta + \sin^2 \theta, we have:

\sin^2 \theta = 1 - \cos^2 \theta \\ \cos^2 \theta = 1 - \sin^2 \theta
\cos 2\theta = 2 \cos^2 \theta - 1 = 1 - 2 \sin^2 \theta

Half-angle identities

Derived from f(\frac{\theta}{2}+\frac{\theta}{2}):

\sin\theta = 2\sin\frac{\theta}{2}\cos\frac{\theta}{2} \\ \cos\theta = 2\cos^2\frac{\theta}{2}-1 = 1-2\sin^2\frac{\theta}{2}
\tan\theta = \frac{2\tan\frac{\theta}{2}}{1-\tan^2\frac{\theta}{2}}

Power reduction identities

\cos^2\theta = \frac{1 + \cos 2\theta}{2}
\sin^2\theta = \frac{1 - \cos 2\theta}{2}

Replace a product with a sum

Derived from the addition formulae above, f(\theta + \phi) \pm f(\theta - \phi). Work backwards from \sin(\theta + \phi) + \sin(\theta - \phi) = 2\sin\theta\cos\theta.

\sin\theta\cos\phi = \frac{1}{2}[\sin(\theta + \phi) + \sin(\theta - \phi)]
\cos\theta\sin\phi = \frac{1}{2}[\sin(\theta + \phi) - \sin(\theta - \phi)]
\cos\theta\cos\phi = \frac{1}{2}[\cos(\theta + \phi) + \cos(\theta - \phi)]
\sin\theta\sin\phi = -\frac{1}{2}[\cos(\theta + \phi) - \cos(\theta - \phi)]

Replace a sum with a product

If x = \theta + \phi and y = \theta - \phi, then x + y = 2\theta and x - y = 2\phi. We can substitute these into f(\theta) \pm f(\phi), starting from \sin\frac{2\theta}{2} + \sin\frac{2\phi}{2}.

\sin\theta + \sin\phi = 2\sin\frac{\theta + \phi}{2}\cos\frac{\theta - \phi}{2}
\sin\theta - \sin\phi = 2\cos\frac{\theta + \phi}{2}\sin\frac{\theta - \phi}{2}
\cos\theta + \cos\phi = 2\cos\frac{\theta + \phi}{2}\cos\frac{\theta - \phi}{2}
\cos\theta - \cos\phi = -2\sin\frac{\theta + \phi}{2}\sin\frac{\theta - \phi}{2}

Another approach is to rewrite f(x) \pm f(y) as f(\theta + \phi) \pm f(\theta - \phi) and expand and simplify from there.

Reciprocal functions

\csc\theta = \frac{1}{\sin\theta}
\sec\theta = \frac{1}{\cos\theta}
\cot\theta = \frac{1}{\tan\theta}

Using 1 = \sin^2\theta + \cos^2\theta, we can see that:

\frac{\sin^2\theta}{\cos^2\theta} + \frac{\cos^2\theta}{\cos^2\theta} = \frac{1}{\cos^2\theta}
\tan^2\theta + 1 = \sec^2\theta

By dividing instead by \sin^2\theta, we get:

1 + \cot^2\theta = \csc^2\theta

Derivatives of trigonometric functions

\begin{aligned} \frac{\dd}{\dx}[\sin\theta] &= \cos\theta \\ \frac{\dd}{\dx}[\cos\theta] &= -\sin\theta \\ \frac{\dd}{\dx}[\tan\theta] &= \sec^2\theta = \cos^{-2}\theta \\ \frac{\dd}{\dx}[\csc\theta] &= -\cos\theta(\sin\theta)^{-2} = -\cot\theta\csc\theta \\ \frac{\dd}{\dx}[\sec\theta] &= \sin\theta(\cos\theta)^{-2} = \tan\theta\sec\theta \\ \frac{\dd}{\dx}[\cot\theta] &= -\sec^2\theta(\tan\theta)^{-2} = -\csc^2\theta \\ \end{aligned}