Mathematics — benbridle.com

When the denominators have a common factor, first separate these out to the side and then multiply by the uncommon factors. This saves time and effort with complex equations. In the following example, x and 3 are the uncommon factors.

\frac{5}{2x} + \frac{y}{6} = \frac{5}{2 \times x} + \frac{y}{2 \times 3} = \frac{5 \times 3}{2 \times x \times 3} + \frac{y \times x}{2 \times 3 \times x}

Exponents

Basic forms

a^0 = 1 \tag{where a is not zero}

a^1 = a

Fractional exponents

a^\frac{b}{c} = (\sqrt[c]{a}) ^ b

Negative exponents

a^{-b} = \frac{1}{a^b} \tag{where a is not zero}

Multiplying exponents

a^b a^c = a^{b+c}

Dividing exponents

\frac{a^b}{a^c} = a^{b-c}

Exponents of exponents

(a^b)^c = a^{bc}

\sqrt{a^b} = a^\frac{b}{2}

Distributive law with exponents

(ab)^c = a^c b^c

\sqrt{ab} = \sqrt{a} \times \sqrt{b}

Notation for roots

The expression \sqrt{x} or x^{\frac{1}{2}} represents the positive square root.
The expression -\sqrt{x} or -(x^{\frac{1}{2}}) represents the negative square root.
The expression \pm\sqrt{x} or \pm(x^{\frac{1}{2}}) represents both square roots.
When asked to ‘solve for x when x^2 = 4, both roots are required.

Multiplying conjugate roots

The conjugate of \sqrt{x} + \sqrt{y} is \sqrt{x} - \sqrt{y}, and vice versa.

(\sqrt{x} + \sqrt{y})(\sqrt{x} - \sqrt{y}) = x - y

Rationalising the denominator

For any fraction with a square root in the denominator, we can lift the square root up to the numerator by multiplying both the numerator and the denominator by the conjugate of the denominator.

\frac{a}{\sqrt{b}} = \frac{a}{\sqrt{b}} \times \frac{\sqrt{b}}{\sqrt{b}} = \frac{a\sqrt{b}}{b}

\frac{a}{\sqrt{b} - \sqrt{c}} = \frac{a}{\sqrt{b} - \sqrt{c}} \times \frac{\sqrt{b} + \sqrt{c}}{\sqrt{b} + \sqrt{c}} = \frac{a(\sqrt{b}+\sqrt{c})}{b - c}

Equations and inequalities

To preserve an equality, any operation performed on one side of the equality must also be performed on the other side.

Notation

x \in (a, b) denotes an open interval (where a < x < b)
x \in [a, b] denotes a closed interval (where a <= x <= b)
Intervals can also be half-open (as x \in (a, b] or vice versa)

Multiplying or dividing by a negative value

When multiplying or dividing an inequality by a negative number, we must reverse the direction of the inequality (the signs of both values flip and they end up on opposite sides of zero).

We can’t multiply or divide an inequality by an unknown term, because the sign of that term isn’t yet known. To deal with this, we use addition and subtraction to rewrite the inequality to have zero on one side, and then we solve to find the values of the unknown terms.

Critical points

A critical point is the argument of a function where the function derivative is zero (a stationary point) or undefined.

A point at which a term changes sign is also called a critical value.

The critical value of an inequality is, say, for x < \frac{1}{2} the critical value will be \frac{1}{2}, because x = \frac{1}{2}.

Solving quadratic equations by factoring

It is much easier to work with and to solve quadratic equations that are in a factored form. The factored form of a quadratic equation is the product of two linear forms:

(ax + b)(cx + d) = (ac)x^2 + (ad + bc)x + (bd) = 0

There’s a visual aid with boxes that can help with finding these linear forms from the expanded polynomial form:

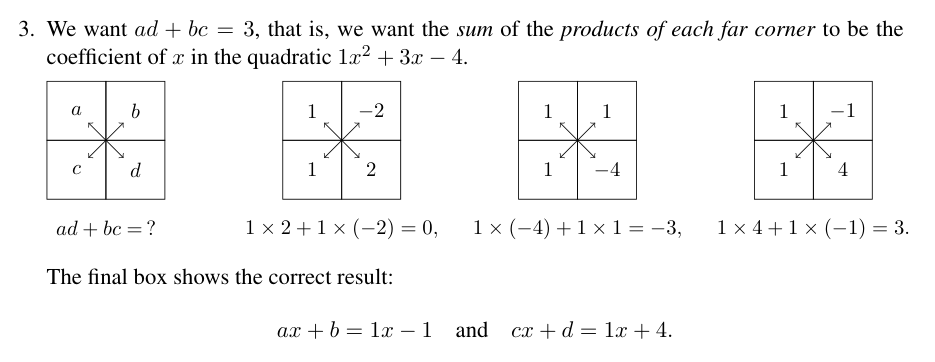
When we solve a quadratic equation, we are finding the values for each variable that will make the equation true. Every quadratic equation will have zero, one, or two real solutions.

We can use the fact that if ab = 0 then a = 0 or b = 0 (or both). Given a factored quadratic equation in the form (ax + b)(cx + d) = 0, we know that either ax + b = 0 or cx + d = 0.

In the example equation x^2 + 3x - 4 = (x+1)(x-4) from above, x = -1 or x = 4.

Solving quadratic equations by completing the square

x^2 + bx + c = (x+\frac{b}{2})^2 - \frac{b^2}{4} + c = 0

If the result is the difference of two squares (so \frac{b^2}{4} - c \geq 0) then we can solve the equation. If, however, the result is the sum of two squares (so \frac{b^2}{4} - c < 0) then the equation has no real solutions.

Once the equation is in the form (x + \frac{b}{2})^2 - \frac{b^2}{4} + c = 0, we can see that (x + \frac{b}{2})^2 = \frac{b^2}{4} - c. To find the solutions of x, we take the square root of both sides and solve for x:

x + \frac{b}{2} = \sqrt{\frac{b^2}{4} - c}

Solving quadratic equations using the quadratic formula

x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}

The coefficients of the polynomial can be substituted into the equation and then solved to directly find the values of x.

The discriminant is the portion b^2 - 4ac beneath the square root, and can be used to determine the number of real solutions. If the discriminant is negative, there are no real solutions to the equation. If it’s zero, there’s one, and if it’s positive, there are two.